Tutorial de Decibel: dB i dBm vs. Gain i Milliwatts

El concepte de decibel (dB) és comprensible i confús per a algú que se li introdueix. La combinació d’especificacions de guany, potència i tensió (i corrent, però no tan sovint) que barregen dB, dBm, dBW, watts, miliwatts, tensió, millivolts, etc., requereix sovint convertir les converses d’anada i tornada entre valors lineals i valors de decibel. Aquest breu tutorial ajudarà a aclarir la diferència entre treballar amb decibels i treballar amb valors lineals.

Els logaritmes (logs) van ser concebuts per primera vegada a les primeres 1600s pel matemàtic escocès John Napier, com una eina per a simplificar les operacions de multiplicació i divisió convertint-les en operacions de suma i resta més ràpides i menys propenses a errors. Això es fa possible a causa de la multiplicació de dos nombres expressats com a números de base similars amb exponents només es pot fer sumant els exponents junts. La divisió d’aquests mateixos nombres s’aconsegueix restant els exponents. És una de les lleis dels exponents, i sembla:

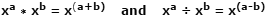
Utilitzant nombres reals com a exemple, on x = 10, a = 4, b = 1:

La llei d’exponents funciona per qualsevol nombre base, no només per 10. Això és:

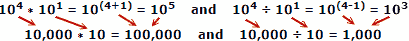
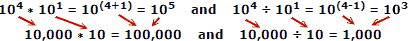
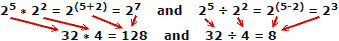
Les persones solen equivocar-se en sumar i restar nombres, de manera que és evident l’avantatge dels logaritmes. Recordeu que els logaritmes es van desenvolupar abans que es disposessin ordinadors mecànics o electrònics automàtics. Una regla de diapositives explota les propietats dels logaritmes per al seu càlcul, però aquest és un tema principal independent.

Aquests són exemples senzills, però valen per a qualsevol base o exponent. En absència d’una calculadora, per ser útil per a l’aplicació general, necessiteu una taula de números i els seus logaritmes equivalents. Les taules de registre primerenques omplien volums, en funció de l'espai entre els números (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3, etc.). La bona notícia per als creadors de taules de logaritmes és que només es necessita una sola "dècada" de números (per exemple, 1 a través de 10), ja que cada dècada precedent o secció és un simple múltiple d'una potència de 10.

Nota: utilitzo la base 10 en aquesta discussió, ja que aquesta és la base del nostre sistema de nombres comú, d'aquí el terme "logaritme comú" per als registres de base 10. Potser heu sentit a parlar de logaritmes naturals, que utilitzen la base de e, però e no s’utilitza molt sovint per calcular la potència elèctrica, la tensió i les quantitats actuals escalars (tot i que s’utilitza quan s’inclouen angles de fase, és a dir, identitat d’Euler). Els logaritmes naturals s’escriuen com a ln (x) sense el subíndex ‘e’, mentre que generalment els logaritmes 10 de base s’escriuen simplement com a log (x) sense el subíndex 10; és a dir, no loge (x) o log10 (x), respectivament.

Per una base = taula de registre 10:

Paper gràfic d'enginyeria semin logarítmica 5 Cycles - RF CafeLa excepció i cas especial és logx (0) = Indefinit. Això és així perquè no hi ha cap poder al qual pugueu elevar cap número i obtenir 0 (zero). Podeu apropar-vos de manera asimptòtica a zero, però no podeu arribar a zero. No apareixerà mai el número zero en una escala de registre; solen passar d'alguna potència de 10 a una altra potència de deu. A la dreta es mostra un exemple de paper gràfic de registre. Disposa de 'cicles' o 'dècades' de 5. Observeu que no hi ha cap zero a l'eix Y.

El logaritme de base d'un nombre 10 (comú) d'un número, doncs, és l'exponent a què cal augmentar 10 per obtenir aquest nombre. És a dir, ja que 10 va augmentar la potència de 2 és igual a 100 (102 = 100), el registre 10 base de 100 és 2 (log10 100 = 2).

Aquesta és la llei bàsica dels logaritmes:


Realitzeu les mateixes multiplicacions i divisions que es fan a la part superior de la pàgina mitjançant els logaritmes reals:



Està bé, però amb el que acabes, és el logaritme del número que busques. Pregunta: A excepció d’un exemple senzill com aquest, com s’obté la resposta que necessiteu? Resposta: busqueu l’antilogaritme (antilog) del resultat. En aquest cas:

Un exemple més dur i molt probable amb números que no siguin potències completes de 10, podria semblar al següent:




 Calculadora HP-35 (wikipedia) - RF CafePer què el logaritme de "x" és igual a 1.8444, l'antilòg és igual a "x", que és 69.9



Vaig utilitzar la meva calculadora per cercar els registres i antilògics d’aquests números, però abans de 1972 quan Hewlett Packard (HP) va introduir la seva calculadora científica HP-35, la persona mitjana sense accés a un ordinador de mainframe corporatiu o universitari que necessitava utilitzar un registre. taula per realitzar aquests càlculs.

A qui es molesta en fer servir els logaritmes avui en dia, podria preguntar? Molta gent, inclosa jo, molt sovint quan calcula paràmetres del sistema en cascada com la xifra de soroll (NF) i els punts d’intercepció (IP). La suma i la resta simples de valors de dB de guany i de potència dBm no funcionen amb NF i IP. Les fórmules de govern utilitzen la multiplicació i la divisió dels valors de guany i lineal de potència, que necessita primer convertir dB i / o dBm en nombres lineals (relació de guany i mW) mitjançant antilògics, realitzar els càlculs en cascada i després convertir el resultat a dB i / o dBm mitjançant registres.

No totes les operacions en cascada del sistema requereixen convertir-se enrere i enrere. Per exemple, si només es necessita el guany total i / o nivell de potència de sortida, es poden realitzar càlculs amb unitats lineals (mW i multiplicadors) o amb unitats logarítmiques (dBm i dB, respectivament).

La definició de "dB" i "dBm"

Un decibel (dB) en enginyeria elèctrica es defineix com 10 vegades el logaritme base 10 d'una relació entre dos nivells de potència; per exemple, Pout / Pin (guany, dit d’una altra manera). Això és:

Per tant, tots els guanys superiors a 1 s’expressen com a decibels positius (> 0) i els guanys inferiors a 1 s’expressen com a decibels negatius (<0). Tingueu en compte que per als casos que trobem la majoria de nosaltres, la proporció lineal de P1 / P2 ha de ser un nombre positiu (> 0) ja que el logaritme de 0 no està definit i el logaritme de nombres negatius són complexos (contenen tant una part real com una part imaginària). ). El valor dB, però, teòricament pot assumir qualsevol valor entre −∞ i + ∞, inclòs 0, que és un guany d'1 [10 * log (1) = 0 dB].

"dBm" és una unitat de potència basada en decibelis que es fa referència a 1 mW. Com que 0 dB de guany és igual a un guany de 1, 1 mW de potència és 0 dB major que 1 mW o 0 dBm. De la mateixa manera, una unitat de potència de dBW és decibels en relació amb 1 W de potència.


En conseqüència, tots els valors de dBm més grans que 0 són majors que 1 mW i tots els valors de dBm inferiors a 0 són menors que 1 mW (vegeu Fig. 1). Per exemple, + 3.01 dBm és 3.01 dB més gran que 1 mW; és a dir, o 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm és 3.01 dB inferior a 1 mW; és a dir, o 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

La taula següent mostra alguns exemples numèrics de manera que podeu veure la correlació entre mW i dBm. El mateix conjunt de valors representats a escala logarítmica produiria una línia recta. A causa de la relació logarítmica, el gràfic agrupa els valors més petits respecte de l'eix vertical esquerre. Per obtenir més claredat, es proporciona una versió magnífica de la regió 0 a 1 mW.

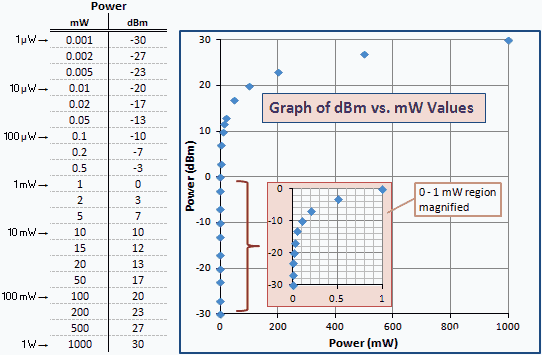
Fig. 1 - Gràfic de potència en unitats de dBm vs. mW

Fig. 2 és una taula i gràfic de dB vs ràtios de guany lineals similars als dBm vs. mW de la Fig. 1. Tingueu en compte que els nombres i les corbes són exactament els mateixos; només es canvien les etiquetes dels eixos. Això és degut a que dBm és una unitat de potència expressada en dB en relació amb 1 mW (0 dBm).

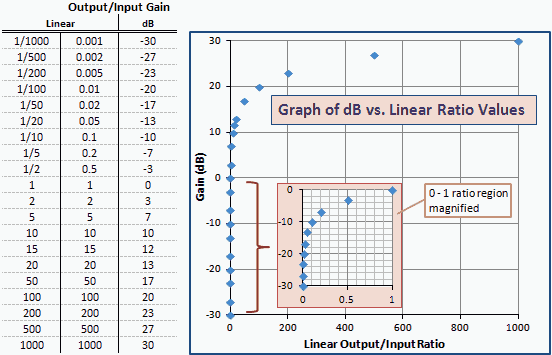
Fig. 2: Gràfic de guany en unitats de dBm vs. relació lineal

Fonamentalment, el guany és un factor de multiplicació (o divisió). Com a exemple, un amplificador pot tenir un benefici que augmenta el senyal per un factor de 4 (és a dir, 4x) d’entrada a sortida (vegeu Fig. 3). Si un senyal 1 mW (0 dBm) és introduït a l'amplificador, llavors 1 mW * 4 = 4 mW surt. En termes de decibels, un factor de 4 equival a 10 * log (4) = 6.02 dB, de manera que 0 dBm a més 6.02 dB de rendiments de guanys + 6.02 dBm a la sortida.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

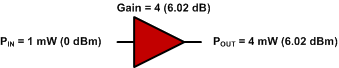
Fig. 3: Plus amplificador.

Combinant guanys (lineals i dB) amb valor positiu

Si un amplificador amb un guany de 4 és en sèrie amb un segon amplificador amb un guany de 6, el guany total és 4 * 6 = 24. En termes de decibels, un factor de 6 equival a 10 * log (6) = 7.78 dB, i un factor de 24 equival a 10 * log (24) = 13.8 dB.

Igual que 4 x 6 = 24 (guany lineal), 6.02 dB + 7.78 dB = 13.8 dB (guany de decibels).

Si un senyal 1 mW (0 dBm) és introduït a l'amplificador, 4 mW surt del primer amplificador i 24 mW surt del segon amplificador. Vegeu Fig. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Fig. 4 - Augment en doble amplificador en cascada

Combinació de guanys i pèrdues (lineal i dB)
Aquest següent exemple mostra què passa quan es troba un guany <1 (una pèrdua), on es posa un atenuador amb un guany de 1/6 després del primer amplificador en lloc de tenir un segon amplificador. Vegeu la figura 5.
4 * 1 / 6 = 2 / 3 (guany lineal). Igualment 6.02 dB - 7.78 dB = −1.76 dB (guany de decibels).
Igual que amb l’exemple anterior, si un senyal 1 mW (0 dBm) s’introdueix a l’amplificador amb un guany de 4, aleshores surt 4 mW. Que 4 mW entra fins a l'atenuador amb un guany lineal de 1 / 6 i surt a un nivell de potència de 4 / 6 mW (2 / 3 mW).
El guany total en aquest cas és 4 / 6 = 2 / 3, de manera que la potència de sortida serà realment inferior a la potència d’entrada.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Fig. 5 - Amplificador en cascada i atenuació.

12 mW + 34 mW + 8 mW + 20 dB

Informació suplementària sobre logaritmes
Logaritmes de productes
Una propietat de logaritmes utilitzada implícitament per sobre de l'estat diu el següent, i és la base per a poder sumar i restar valors del logaritme en lloc de multiplicar els seus equivalents lineals.

"h * j / k * m / n" pot representar una cascada de components que tenen tres dispositius (h, j i m) cadascun amb guany> 1 i dos dispositius (k i n) cadascun amb un guany <1 (vegeu Fig. 6). El guany total del sistema es pot calcular multiplicant tots els valors de guany lineals o sumant tots els valors de guany de decibels.

Fig. 6 - Components en cascada

Logaritmes d’exponents
El següent és important per comprendre per què el guany d'energia en termes de potència és 10 * log (Pout / Pin) dB, mentre que la pujada en termes de tensió és 20 * log (Vout / Vin) dB.


que és així perquè cf és igual a c multiplicat per si mateix per f. Per exemple, si f = 4:


Rendiment de potència basat en potencia vs guany de potència basat en voltatge
El guany de potència és Pout / Pin i el guany de tensió és Vout / Vin. El guany de potència basat en una relació de potència en decibels es defineix com 10 * log (Pout / Pin). El guany de potència en termes de tensió és [(Vout2 / R) / (Vin2 / R)], ja que segons la llei de Ohm P = V2 / R. La "R" dels denominadors cancel·la la sortida de Vout2 / Vin2, que és igual a (Vout / Vin) 2, tal com es defineix per la regla dels exponents que diu ac / bc = (a / b) c. D’aquí:

Nota important: L’augment de tensió en termes de tensió és 10 * log (Vout / Vin) dB, el mateix que amb la pujada d’energia en termes de potència. Només és quan s'aplica l'equació de 20 * log (Vout / Vin) dB quan es produeix un increment d'energia en termes de tensió. Aquest és un punt comú de confusió.


Cap operació en matemàtiques és arbitrària, i això val per què una pèrdua de potència del senyal (guany <1) es representa com un valor negatiu i, per tant, es resta durant un càlcul en cascada. És una demostració senzilla, però digna d’esmentar.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Si voleu crear una emissora de ràdio, potencieu el transmissor de ràdio FM o necessiteu qualsevol altre Equip FM, Si us plau, no dubti en contactar amb nosaltres: [protegit per correu electrònic].

Deixa un missatge 

Llista de missatges